为了帮助广大考生更好备战2015年上海三支一扶考试，华智公务员第一时间为各位考生提供备考指导，对上海三支一扶行测考试中的各个详细问题作出详细解答，同时还对一些知识进行了总结和梳理，希望能给广大考生带来一定的帮助!

行程问题是三支一扶考试的重点题型，由于行程问题是一种较为成熟的题型，所以这部分题相对来说难度较大。解决行程问题主要用到的方法是：比例思想、特值思想、数形结合和方程思想。对于这部分知识，重点从两个角度进行学习和掌握：一是对核心公式的掌握和理解;二是对常见模型的掌握。这里华智教育专家介绍一些行程问题的基础知识。

一、 核心公式。

理解性记忆：同向变化是正比关系，反向变化是反比关系，具体情况为：路程一定，速度越大，所用的时间越少 ;速度一定，时间越长，路程越远;时间一定，速度越大，所走的路程越远。

例：A、B两地分别有甲、乙两个人，相向而行，已知甲的速度是乙速度的

，相遇时甲比乙多走了200米，求A、B之间的距离?

【华智解析】方法一：列方程：设甲的速度为

，则乙的速度为

，走的时间为

，则

所以

方法二：正比法：由于题中条件可知，时间一定，

所以

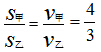
，即甲走4份路程，乙走3份路程，甲比乙多的1份路程等于200米，甲乙共走7份路程等于7×200=1400。

正反比关系在解决行程问题时能够提高做题效率，省去很多计算步骤。很方便应用，一定要掌握。

二、简单的相遇、追击问题

1、相遇问题：关于直线相遇，题目中通常会说A、B两地分别有甲、乙两人面对面行驶……这里要注意的是相向就是面对面的意思，另外，两人在同一条直线上面对面行驶一定会相遇，并且当他们相遇时所用的时间一定相同，即两个人走的时间一样，所以AB总长就是甲、乙二人的路程和，它应该等于甲的路程加上乙的路程，即

叫做速度和。所以直线相遇的模型：路程和等于速度和乘以时间，必须要强调的是，这个公式运用的前提条件为：甲、乙运行时间相同是一致的且相向运行。随着应用的深入，现在相遇公式应用更为普遍，只要时间一定，两个人的路程和一定等于速度和乘以时间。

关于环形相遇，通常给出的模型都是在同一跑道上，甲乙二人从同一地点背向行驶……显然他们是能够相遇的，并且当他们相遇时，他们所走的路程和应该是圆的周长，当他们第二次相遇时，其路程和应该是两个圆的周长，以此类推，第N次相遇时，其路程和是N个圆的周长，所以环形相遇问题，路程和与圆的周长有关，具体的关系要根据具体的情景而定。当他们相遇时，所用时间仍是相同的，所以仍可用：路程和等于速度和乘以时间。

2、追击问题：对于直线追击，题目中通常会说甲、乙两人在A、B两地同时向同一方向行驶(B点在前A点在后即乙在甲的前方且甲的速度大于乙的速度)，到C点甲追上乙。这里要注意的几点：一是同一方向也叫同向;二是后者的速度一定大于前者的速度，这样才能追上。另外，在追击过程中，一定同时出发，到某一时刻追上，因此，他们所用时间仍然是相同的，此时的AB就应该是路程差了，即AB = AC-BC=S甲-S乙=V甲t+V乙t=(V甲+V乙)t即路程差等于速度差乘以时间。需要强调的是，只有两人所用时间相同才能用这个公式。

关于环形追击，通常会这样给出：甲、乙二人在环形跑道上同一点同时同向出发，其中甲的速度大于乙的速度……同向行驶，所以是个追及问题，由于甲的速度大，所以这里实际上是甲在追乙，当甲追上乙时，相当于是甲比乙多跑了一圈，这也就是平时我们所说的套圈问题，当甲第二次追上乙时，甲比乙多跑了两圈，以此类推，甲第N次追上乙时，甲比乙多跑了N圈，所以环形追及问题中路程差与圆的周长有关，具体的关系要根据具体的情景而定。当甲追上乙时，他们所用时间仍是相同的，所以仍可用：路程差等于速度差乘以时间 。

总结：相遇 ：路程和=速度和×时间;

直线相遇路程与A、B两点距离有关;

环形相遇路程与圆的周长有关。

追击： 路程差=速度差×时间;

直线追击路程与A、B两点距离有关;

环形追击路程与圆的周长有关。

注意：公式能直接用的前提是所用时间相同。